코리올리 효과

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요

코리올리 효과는 회전하는 기준틀에서 물체의 운동 방향에 수직으로 작용하는 겉보기 힘이다. 이 힘은 물체의 속도와 회전하는 좌표계의 각속도에 따라 결정되며, 관성력의 일종이다. 코리올리 효과는 17세기부터 연구되었으며, 레온하르트 오일러, 피에르 시몽 라플라스 등에 의해 수학적으로 설명되었다.

코리올리 효과는 지구의 자전에 의해 발생하는 현상으로, 기상학, 해양학, 물리학 등 다양한 분야에서 나타난다. 지구에서는 북반구에서 진행 방향의 오른쪽, 남반구에서는 왼쪽으로 물체의 운동 방향을 휘게 한다. 이러한 영향은 저기압과 고기압의 순환, 해류의 흐름, 태풍의 발생 등에 영향을 미치며, 푸코의 진자와 같은 현상에서도 관찰된다. 또한, 유량계, 분자 물리학, 곤충의 비행, 라그랑주점의 안정성 등 다양한 분야에서 응용되고 있다.

2. 역사

코리올리 효과는 17세기부터 과학자들에 의해 연구되기 시작했다. 19세기 프랑스 과학자 가스파르 구스타브 코리올리는 이 효과를 수학적으로 처음 기술했다.^[7]

19세기 후반에는 기단이 등압선을 따라 움직이게 하는 힘인 기압 경도력과 코리올리 힘의 대규모 상호 작용이 완전히 이해되었다.^[15]

2. 1. 초기 연구

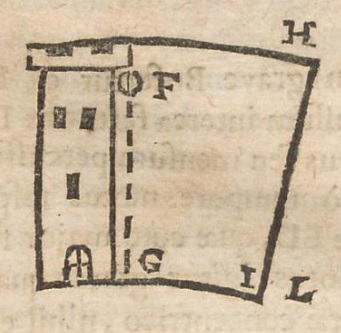
1651년 이탈리아 과학자 조반니 바티스타 리치올리와 그의 조수 프란체스코 마리아 그리말디는 대포와 관련하여 코리올리 효과를 설명하면서, 지구 자전으로 인해 북쪽으로 발사된 대포알이 동쪽으로 휘어져야 한다고 ''Almagestum Novum''에 기술했다.^[2] 1674년 클로드 프랑수아 밀리에 드샬은 그의 저서 ''Cursus seu Mundus Mathematicus''에서 지구 자전이 낙하하는 물체와 행성의 극점을 향해 발사된 발사체의 궤적에 편향을 일으켜야 한다고 설명했다. 리치올리, 그리말디, 그리고 드샬은 모두 코페르니쿠스의 지동설에 반대하는 주장의 일환으로 이 효과를 설명했다. 즉, 그들은 지구 자전이 이 효과를 만들어야 한다고 주장했고, 따라서 이 효과를 감지하지 못한 것은 지구가 정지해 있다는 증거라고 주장했다.^[3] 코리올리 가속도 방정식은 1749년 레온하르트 오일러에 의해 유도되었고,^[4]^[5] 이 효과는 1778년 피에르 시몽 라플라스의 조석 방정식에서 설명되었다.^[6]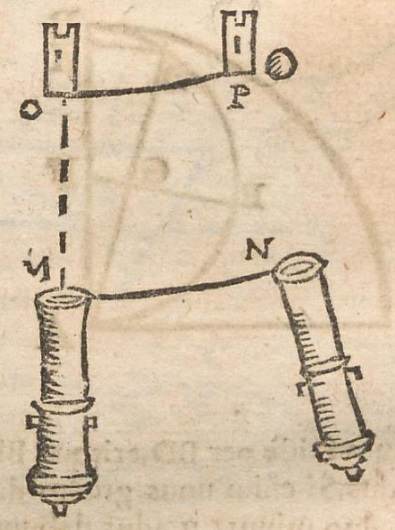

데샬의 ''Cursus seu Mundus Mathematicus''(1674)에 나오는 그림. 회전하는 지구에서 대포알이 목표 지점 오른쪽으로 휘어지는 모습을 보여준다. 대포알의 오른쪽 방향 운동이 탑의 운동보다 빠르기 때문이다.

데샬의 ''Cursus seu Mundus Mathematicus''(1674)에 나오는 그림. 회전하는 지구에서 탑에서 떨어지는 공의 모습을 보여준다. 공은 ''F''에서 떨어진다. 탑의 꼭대기는 밑바닥보다 더 빠르게 움직이므로, 공이 떨어지는 동안 탑의 밑바닥은 ''I''로 움직이지만, 탑의 꼭대기와 같은 동쪽 방향 속도를 가진 공은 탑의 밑바닥보다 더 빨리 움직여 ''L''에서 더 동쪽으로 떨어진다.

2. 2. 코리올리의 연구

가스파르 구스타브 드 코리올리(Gaspard-Gustave de Coriolis)는 1835년 물레방아와 같이 회전하는 부분이 있는 기계의 에너지 수율에 대한 논문을 발표했다.^[7] 이 논문에서 코리올리는 회전하는 기준틀에서 감지되는 보조적인 힘을 고려했다. 코리올리는 이러한 보조적인 힘을 두 가지 범주로 나누었다. 두 번째 범주에는 좌표계의 각속도와 입자의 속도를 계의 회전축에 수직인 평면으로 투영한 것의 외적에서 발생하는 힘이 포함되었다. 코리올리는 이미 첫 번째 범주에서 고려된 원심력과의 유사성 때문에 이 힘을 "복합 원심력"이라고 불렀다.^[9] 이 효과는 20세기 초에는 "코리올리 가속도"로,^[11] 1920년대에는 "코리올리 힘"으로 알려졌다.^[12]

1856년 윌리엄 페렐(William Ferrel)은 코리올리 힘에 의해 공기가 편향되어 우세한 편서풍을 생성하는 중위도의 순환 세포의 존재를 제안했다.^[13]

3. 정의

코리올리 효과는 회전하는 좌표계에서 운동하는 물체에 작용하는 가상의 힘이다. 이 힘은 프랑스의 과학자 가스파르 귀스타브 코리올리의 이름에서 따왔다. 회전하는 좌표계에서는 물체가 직선으로 움직이는 것처럼 보이지만, 실제로는 곡선 경로를 따라 움직이게 된다. 이는 회전하는 좌표계 자체가 회전하고 있기 때문에 발생하는 현상이다.

3. 1. 코리올리 효과

그림 1: 각운동량 보존 법칙에 의해 회전판의 붉은 점에서 보았을 때 물체는 진행 방향의 왼쪽으로 움직이는 것처럼 보인다.

코리올리 힘은 각운동량 보존 법칙에 의해 발생한다. 회전하는 좌표계 내에서 물체가 운동할 때, 회전축에 대한 반지름이 변하면 속도가 변하게 되고, 이로 인해 코리올리 힘이 발생한다. 회전하는 좌표계 내에서 물체가 운동을 하는 경우 회전축에 대해 반지름이 줄어드는 경우에는 줄어드는 반지름에 대해 속도가 변화하게 된다. 이 결과 회전좌표계는 코리올리 힘과, 가로힘이 발생한다. 코리올리 힘의 크기는 다음과 같이 주어진다.

:

\mathbf{F_{Coriolis}} = 2m\left(\mathbf{v} \times \mathbf{\Omega}\right)

뉴턴 역학에서 관성 기준틀에 있는 물체의 운동 방정식은 다음과 같다.

:

\boldsymbol{F} = m\boldsymbol{a}

여기서

\boldsymbol{F}

는 물체에 작용하는 물리적 힘의 벡터 합,

m

은 물체의 질량,

\boldsymbol{a}

는 관성 기준틀에 대한 물체의 가속도이다.

원점을 지나는 고정된 축을 중심으로 회전하는, 회전 속도가 변하는 기준틀로 이 방정식을 변환하면 다음과 같은 형태가 된다.^[8]^[16]

:

\begin{align}\boldsymbol{F'} &=\boldsymbol{F} - m\frac{\mathrm{d} \boldsymbol{\omega}}{\mathrm{d}t}\times\boldsymbol{r'} - 2m \boldsymbol{\omega}\times \boldsymbol{v'} - m\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r'})  \\& = m\boldsymbol{a'}\end{align}

여기서 ''프라임''(') 변수는 회전 기준틀의 좌표를 나타내며(미분이 아님),

$\boldsymbol{F}$ 는 물체에 작용하는 물리적 힘의 벡터 합
$\boldsymbol{\omega}$ 는 관성 기준틀에 대한 회전 기준틀의 각속도
$\boldsymbol{r'}$ 는 회전 기준틀에 대한 물체의 위치 벡터
$\boldsymbol{v'}$ 는 회전 기준틀에 대한 물체의 속도
$\boldsymbol{a'}$ 는 회전 기준틀에 대한 물체의 가속도

회전 틀에서 인지되는 겉보기 힘은 실제 외부 힘과 마찬가지로 겉보기 가속도에 기여하는 추가적인 힘으로 작용한다.^[17]^[18]^[19] 방정식의 겉보기 힘 항은 왼쪽에서 오른쪽으로 읽으면 다음과 같다.^[20]

오일러 힘, $-m \frac{\mathrm{d}\boldsymbol{\omega}}{\mathrm{d}t} \times\boldsymbol{r'}$
코리올리 힘, $-2m ( \boldsymbol{\omega} \times \boldsymbol{v'} )$
원심력, $-m\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r'})$

이 공식에서 볼 수 있듯이 오일러 힘과 원심력은 물체의 위치 벡터

\boldsymbol{r'}

에 의존하는 반면, 코리올리 힘은 회전 기준틀에서 측정한 물체의 속도

\boldsymbol{v'}

에 의존한다. 예상대로, 비회전 관성 기준틀

(\boldsymbol\omega=0)

의 경우 코리올리 힘과 다른 모든 겉보기 힘은 사라진다.^[21]

코리올리 힘은 두 벡터의 외적에 비례하므로, 이 경우 물체의 속도와 좌표계의 회전 벡터 모두에 수직이다. 따라서 다음과 같다.

속도가 회전축과 평행하면 코리올리 힘은 0이다. 예를 들어 지구에서는 적도에 있는 물체가 지구 표면에 대해 북쪽이나 남쪽으로 이동할 때 이러한 상황이 발생한다.
속도가 축을 향해 직선으로 안쪽으로 향하면 코리올리 힘은 국지적 회전 방향과 같다. 예를 들어 지구에서는 적도에 있는 물체가 아래로 떨어질 때 이러한 상황이 발생하며, 떨어지는 공은 탑보다 동쪽으로 더 멀리 이동한다.
속도가 축에서 직선으로 바깥쪽으로 향하면 코리올리 힘은 국지적 회전 방향과 반대이다. 탑의 예에서 위로 발사된 공은 서쪽으로 이동한다.
속도가 회전 방향이면 코리올리 힘은 축에서 바깥쪽으로 향한다. 예를 들어 지구에서는 적도에 있는 물체가 지구 표면에 대해 동쪽으로 이동할 때 이러한 상황이 발생한다. 표면의 관찰자에게는 위로 이동하는 것처럼 보일 것이다.
속도가 회전 방향과 반대이면 코리올리 힘은 축 안쪽으로 향한다. 예를 들어 지구에서는 적도에 있는 물체가 서쪽으로 이동할 때 이러한 상황이 발생하며, 관찰자에게는 아래로 휘어지는 것처럼 보일 것이다.

코리올리 힘의 기원을 직관적으로 설명하기 위해, 지구 표면을 따라 움직이며 북반구에서 북쪽으로 이동하는 물체를 생각해 보자. 우주에서 보면, 이 물체는 정확히 북쪽으로 이동하는 것처럼 보이지 않고 동쪽으로의 운동(지구 표면과 함께 오른쪽으로 회전)을 가지고 있다. 물체가 더 북쪽으로 이동할수록, "평행선(위도)의 반지름"이 작아지고, 따라서 표면의 동쪽 방향 운동이 느려진다. 물체가 북쪽으로 이동하면서, 처음 시작했던 동쪽 방향 속도를 유지하려는 경향이 있으므로, 동쪽(즉, 초기 운동의 오른쪽)으로 방향을 바꾼다.^[23]^[24]

북쪽으로의 운동을 고려한 이 예에서 명확하지 않지만, 수평 방향의 편향은 동쪽이나 서쪽(또는 다른 어떤 방향)으로 움직이는 물체에도 동일하게 발생한다.^[25] 그러나 코리올리 효과가 가정용 욕조, 싱크대 또는 변기에서 물이 빠지는 회전을 결정한다는 이론은 현대 과학자들에 의해 반복적으로 반박되었다. 이 힘은 회전에 영향을 미치는 다른 많은 요인들에 비해 무시할 만큼 작다.^[26]^[1]^[27]

위 그림은 반시계 방향으로 회전하는 회전목마의 12시 방향에서 중앙으로 던져진 공을 보여준다. 왼쪽에는 회전목마 위에 정지해 있는 관찰자가 본 공의 모습으로, 공은 중앙으로 직선으로 이동하고 공을 던진 사람은 회전목마와 함께 반시계 방향으로 회전한다. 오른쪽에는 회전목마와 함께 회전하는 관찰자가 본 공의 모습으로, 공을 던진 사람은 12시 방향에 머물러 있는 것처럼 보인다.

회전목마의 조감도. 회전목마는 시계 방향으로 회전한다. 회전목마와 함께 회전하는 회전 중심에 있는 카메라의 관점(왼쪽)과 관성(정지) 관찰자의 관점(오른쪽)에서 본 모습이 나타나있다. 두 관찰자 모두 특정 시점에 공이 회전 중심에서 얼마나 떨어져 있는지는 동의하지만, 방향에 대해서는 동의하지 않는다. 시간 간격은 발사에서 바운스까지의 시간의 1/10이다.

위 그림은 회전판에서 던진 공이 회전목마 가장자리에서 튀어 나와 공을 던진 사람에게 돌아오는 더 복잡한 상황을 설명한다. 코리올리 힘이 궤적에 미치는 영향은 두 관찰자, 즉 회전목마와 함께 회전하는 관찰자와 관성 관찰자의 관점에서 다시 보여준다.

지구 표면 위를 "미끄러지는" 공기의 운동에 영향을 미치는 가속도는 코리올리 항의 수평 성분이다.

:

-2 \, \boldsymbol{\omega \times  v}

이 성분은 지구 표면 위의 속도에 수직이며 다음 식으로 주어진다.

:

\omega \, v\  2 \, \sin \phi

여기서

$\omega$ 는 지구의 자전 속도이다.
$\phi$ 는 위도이며, 북반구에서는 양수이고 남반구에서는 음수이다.

위도가 양수인 북반구에서는, 위에서 보았을 때 이 가속도는 운동 방향의 오른쪽으로 향한다. 반대로 남반구에서는 왼쪽으로 향한다.

위도 φ에서의 좌표계. x축은 동쪽, y축은 북쪽, z축은 위쪽(즉, 구의 중심에서 바깥쪽으로 방사형)

북-남 축을 중심으로 회전하는 구체 위 위도 φ의 위치를 고려해 보자. 국지 좌표계는 x축이 동쪽으로 수평을 이루고, y축이 북쪽으로 수평을 이루며, z축이 수직으로 위쪽을 향하도록 설정한다. 이 국지 좌표계에서 표현된 회전 벡터, 이동 속도, 코리올리 가속도는 다음과 같다.^[33]

:

\boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ \cos \varphi \\ \sin \varphi \end{pmatrix}\ ,

\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ ,

:

\boldsymbol{ a}_C =-2\boldsymbol{\Omega \times v}= 2\,\omega\, \begin{pmatrix} v_n \sin \varphi-v_u \cos \varphi \\ -v_e \sin \varphi \\ v_e \cos\varphi\end{pmatrix}\ .

대기 또는 해양 역학을 고려할 때, 수직 속도는 작고, 코리올리 가속도의 수직 성분은 중력 가속도에 비해 작다. 이러한 경우, 수평 성분만 중요하다. 위 식을 수평면으로 제한하면:

:

\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n\end{pmatrix}\ ,

\boldsymbol{ a}_c = \begin{pmatrix} v_n \\ -v_e\end{pmatrix}\ f\ ,

여기서

f = 2 \omega \sin \varphi \,

는 코리올리 파라미터라고 한다.

''v_n'' = 0으로 설정하면 (양의 φ 및 ω에 대해) 동쪽 방향의 이동은 남쪽 방향의 가속도를 초래함을 즉시 알 수 있다. 마찬가지로, ''v_e'' = 0으로 설정하면 북쪽 방향의 이동은 동쪽 방향의 가속도를 초래한다. 일반적으로, 수평적으로 관찰하면, 가속도를 유발하는 운동의 방향을 따라 보면, 가속도는 항상 수평 방향에 관계없이 오른쪽으로 90° 회전하고 크기가 같다.

적도 운동의 경우, φ = 0°로 설정하면:

:

\boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\ ,

\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ ,

\boldsymbol{ a}_C = -2\boldsymbol{\Omega \times v} = 2\,\omega\, \begin{pmatrix} -v_u \\0 \\ v_e \end{pmatrix}\ .

이 경우 '''Ω'''는 북-남 축과 평행하다.

따라서 동쪽 방향의 운동은 에트뵈시 효과라고 알려진 위쪽 방향의 가속도를 제공하고, 위쪽 방향의 운동은 서쪽 방향의 가속도를 생성한다.

코리올리 효과로 인해 북반구의 저기압계는 반시계 방향으로 회전하고, 남반구의 저기압계는 시계 방향으로 회전한다.

북반구 저기압 영역 주변의 흐름을 나타낸 개략도. 로스비 수가 낮으므로 원심력은 거의 무시할 수 있다. 기압 경도력은 파란색 화살표로, 코리올리 가속도는 빨간색 화살표로 표시되어 있다.

다른 힘이 없을 때 공기 덩어리의 관성 원을 나타낸 개략도. 풍속 약 에서 로 계산되었다.

아폴로 17호에서 촬영한 유명한 지구 사진 속 구름 형성은 유사한 순환을 직접 보여준다.

코리올리 효과의 가장 중요한 영향은 해양과 대기의 대규모 역학이다. 해양학에서는 지구가 정지해 있는 회전 좌표계를 가정하는 것이 편리하다. 이러한 임시 가정을 수용하기 위해 원심력과 코리올리 힘이 도입된다. 그들의 상대적 중요성은 적용 가능한 로스비 수에 의해 결정된다.

표층 해류는 바람이 수면 위로 이동함으로써 발생하기 때문에, 코리올리 힘은 해류와 사이클론의 이동에도 영향을 미친다. 코리올리 효과의 힘이 강할수록 바람이 더 빨리 회전하고 추가 에너지를 얻어 허리케인의 강도가 증가한다.

고기압계 내의 공기는 코리올리 힘이 안쪽으로 향하는 방향으로 회전하고, 거의 바깥쪽으로 향하는 기압 경도력과 균형을 이룬다. 결과적으로 북반구의 고기압 주변에서는 시계 방향으로, 남반구에서는 반시계 방향으로 공기가 이동한다. 저기압 주변의 공기는 반대 방향으로 회전하여 코리올리 힘이 바깥쪽으로 향하고 안쪽으로 향하는 기압 경도력과 거의 균형을 이룬다.

대기 중에 저기압 영역이 형성되면 공기는 그쪽으로 흘러들어가려는 경향이 있지만, 코리올리 힘에 의해 속도에 수직으로 휘어진다. 그러면 원형 운동 또는 사이클론성 흐름을 만드는 평형 시스템이 형성될 수 있다. 로스비 수가 낮기 때문에 힘의 균형은 저기압 영역을 향하는 기압경도력과 저기압 중심에서 멀어지는 코리올리 힘 사이에서 크게 결정된다.

기압 경도를 따라 흐르는 대신, 대기와 해양의 대규모 운동은 기압 경도에 수직으로 발생하는 경향이 있다. 이것을 지균풍이라고 한다.^[38] 자전하지 않는 행성에서는 유체가 가장 직선적인 경로를 따라 흐르며 기압 경도를 빠르게 제거한다. 따라서 지균 평형은 "관성 운동"의 경우와 매우 다르며, 이것이 중위도 사이클론이 관성 원 운동보다 규모가 훨씬 큰 이유를 설명한다.

이러한 편향 패턴과 이동 방향을 바이알롯 법칙이라고 한다. 대기에서는 흐름 패턴을 사이클론이라고 한다. 북반구에서는 저기압 영역 주변의 이동 방향이 시계 반대 방향이다. 남반구에서는 회전 역학이 거울상이기 때문에 이동 방향이 시계 방향이다.^[39] 적도에서는 코리올리 효과가 약하기 때문에 사이클론이 거의 발생하지 않는다.^[41]

코리올리 힘만 작용하는 속도

v\,

로 움직이는 공기 또는 물의 덩어리는 ''관성원''이라고 하는 원형 궤적을 따라 이동한다. 힘이 입자의 운동 방향에 대해 직각으로 작용하기 때문에, 입자는 반지름

R

인 원을 일정한 속도로 이동하는데, 이 반지름은 다음과 같이 주어진다.

:

R = \frac{v}{f}

여기서

f

는 코리올리 매개변수

2 \Omega \sin \varphi

이며(

\varphi

는 위도), 질량이 완전한 원을 완성하는 데 걸리는 시간은 따라서

2\pi/f

이다. 코리올리 매개변수는 중위도에서 일반적으로 약 10⁻⁴ s⁻¹의 값을 가지므로, 전형적인 대기 속도 10m/s의 경우 반지름은 100km이고 주기는 약 17시간이다. 전형적인 속도가 10cm/s인 해류의 경우, 관성원의 반지름은 1km이다. 이러한 관성원은 북반구에서는 시계 방향이고 남반구에서는 시계 반대 방향이다.

회전계가 포물선 회전판인 경우,

f

는 일정하고 궤적은 정확한 원이 된다. 회전하는 행성에서는

f

가 위도에 따라 변하고 입자의 경로는 정확한 원을 형성하지 않는다. 매개변수

f

가 위도의 사인 함수로 변하기 때문에, 주어진 속도와 관련된 진동의 반지름은 극지방에서 가장 작고 적도 방향으로 증가한다.^[42]

코리올리 효과는 대규모 해양 및 대기 순환에 큰 영향을 미쳐 제트 기류와 서쪽 경계류와 같은 뚜렷한 특징을 형성한다. 코리올리 가속도는 또한 로스비 파와 켈빈 파를 포함한 해양과 대기에서 여러 유형의 파동의 전파에도 영향을 미친다. 또한 해양의 에크만 역학과 스베르드룹 균형이라고 하는 대규모 해류 패턴의 형성에도 중요한 역할을 한다.

적도를 따라 마찰 없는 철로를 달리는 기차를 상상해 보자. 이 기차가 하루 만에 지구를 한 바퀴 도는 데 필요한 속도로 움직인다고 가정하자.^[47] 코리올리 효과는 기차가 서쪽으로 이동할 때, 정지해 있을 때, 그리고 동쪽으로 이동할 때 세 가지 경우에 대해 고려할 수 있다.

# 기차가 서쪽으로 이동하는 경우: 이 경우 기차는 회전 방향과 반대로 움직인다. 따라서 지구의 회전 좌표계에서 코리올리 항은 회전축(아래쪽)을 향해 안쪽으로 향한다. 이 추가적인 아래쪽 힘은 기차가 그 방향으로 움직일 때 무게가 더 무겁게 만든다.

# 기차가 정지하는 경우: 지구의 회전 좌표계에서 기차의 속도는 0이므로 코리올리 힘도 0이고 기차와 승객은 평소 무게를 회복한다.

# 기차가 동쪽으로 이동하는 경우: 이 경우 기차는 지구의 회전 좌표계 방향으로 움직이기 때문에 코리올리 항은 회전축(위쪽)에서 바깥쪽으로 향한다. 이 위쪽 힘은 기차가 정지해 있을 때보다 더 가볍게 보이게 만든다.

이는 또한 서쪽으로 이동하는 고속 발사체가 아래로 편향되고 동쪽으로 이동하는 발사체가 위로 편향되는 이유를 설명한다. 코리올리 효과의 이 수직 성분을 에트뵈시 효과라고 한다.^[48]

매우 얕은 포물면 위를 마찰 없이 움직이는 물체. 물체는 타원 궤적을 따르도록 방출되었다.
''왼쪽'': 관성적 관점
''오른쪽'': 공동 회전 관점

곡면에서 작용하는 힘
''빨간색'': 중력
''녹색'': 수직항력
''파란색'': 알짜 구심력.

코리올리 효과를 보여주기 위해 포물선 회전판을 사용할 수 있다.

평평한 회전판에서는 공동 회전하는 물체의 관성으로 인해 가장자리로 밀려난다. 그러나 회전판 표면이 적절한 포물면 모양을 하고 해당 속도로 회전하면 그림에 표시된 힘 성분 때문에 그릇 표면에 접하는 중력 성분이 물체가 속도와 곡률 반지름으로 회전하는 데 필요한 구심력과 정확히 같아진다. 이렇게 신중하게 윤곽이 잡힌 표면을 통해 코리올리 힘을 독립적으로 표시할 수 있다.^[62]^[63]

어떤 의미에서 지구는 이러한 회전판과 유사하다.^[64] 자전으로 인해 행성은 구체 모양으로 자리 잡았으며, 수직 항력, 중력 및 원심력이 "수평" 표면에서 서로 정확히 균형을 이룬다.

지구 자전으로 인한 코리올리 효과는 푸코 진자의 운동을 통해 간접적으로 볼 수 있다.

코리올리 효과를 실감하려면, 피겨 스케이터처럼 회전하면서, 추를 든 손을 앞으로 뻗었다가 가슴에 가져다 대는 동작을 반복하면 이해하기 쉽다. 왼쪽으로 회전하는 경우, 팔을 앞으로 뻗을 때는 추가 오른쪽으로 당겨지는 듯한 느낌이 들고, 팔을 가슴에 가져다 댈 때는 왼쪽으로 빨려 들어가는 듯한 느낌이 든다. 이처럼, 추의 진행 방향에서 보아 오른쪽으로 치우치는 방향으로 작용하는 것처럼 보이는 힘이 바로 코리올리 힘이다.

코리올리 효과를 공학적으로 이용한 장치로는, 각속도를 측정하는 자이로나 유량계 등이 있다.

4. 발생 원인

코리올리 힘은 회전 좌표계에서 물체의 운동을 기술할 때 나타나는 가상의 힘이다.^[16] 뉴턴 역학에서 관성 기준틀에 있는 물체의 운동 방정식은 다음과 같다.

: $\boldsymbol{F} = m\boldsymbol{a}$

여기서 $\boldsymbol{F}$ 는 물체에 작용하는 물리적 힘의 벡터 합, $m$ 은 물체의 질량, $\boldsymbol{a}$ 는 관성 기준틀에 대한 물체의 가속도이다.

이 방정식을 원점을 지나는 고정된 축을 중심으로 회전하는, 회전 속도가 변하는 기준틀로 변환하면 다음과 같은 형태가 된다.^[16]

: $\begin{align}\boldsymbol{F'} &=\boldsymbol{F} - m\frac{\mathrm{d} \boldsymbol{\omega}}{\mathrm{d}t}\times\boldsymbol{r'} - 2m \boldsymbol{\omega}\times \boldsymbol{v'} - m\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r'}) \\& = m\boldsymbol{a'}\end{align}$

여기서 '프라임'(') 변수는 회전 기준틀의 좌표를 나타내며(미분이 아님),

$\boldsymbol{F}$ 는 물체에 작용하는 물리적 힘의 벡터 합
$\boldsymbol{\omega}$ 는 관성 기준틀에 대한 회전 기준틀의 각속도
$\boldsymbol{r'}$ 는 회전 기준틀에 대한 물체의 위치 벡터
$\boldsymbol{v'}$ 는 회전 기준틀에 대한 물체의 속도
$\boldsymbol{a'}$ 는 회전 기준틀에 대한 물체의 가속도

회전 틀에서 인지되는 겉보기 힘은 실제 외부 힘과 마찬가지로 겉보기 가속도에 기여하는 추가적인 힘으로 작용한다.^[17]^[18]^[19] 방정식의 겉보기 힘 항은 왼쪽에서 오른쪽으로 읽으면 오일러 힘, 코리올리 힘, 원심력 순서이다.^[20]

이 공식에서 볼 수 있듯이 오일러 힘과 원심력은 물체의 위치 벡터

\boldsymbol{r'}

에 의존하는 반면, 코리올리 힘은 회전 기준틀에서 측정한 물체의 속도

\boldsymbol{v'}

에 의존한다. 비회전 관성 기준틀

(\boldsymbol\omega=0)

의 경우 코리올리 힘과 다른 모든 겉보기 힘은 사라진다.^[21]

위 그림은 반시계 방향으로 회전하는 회전목마의 12시 방향에서 중앙으로 던져진 공을 보여준다. 왼쪽에는 회전목마 위에 정지해 있는 관찰자가 본 공의 모습으로, 공은 중앙으로 직선으로 이동하고 공을 던진 사람은 회전목마와 함께 반시계 방향으로 회전한다. 오른쪽에는 회전목마와 함께 회전하는 관찰자가 본 공의 모습으로, 공을 던진 사람은 12시 방향에 머물러 있는 것처럼 보인다. 회전하는 관찰자는 공의 궤적이 곡선으로 나타나는데, 이는 원심력과 코리올리 힘을 결합해야 설명할 수 있다.

4. 1. 회전 좌표계

회전 좌표계는 관성 좌표계에 대해 일정한 각속도로 회전하는 좌표계이다. 회전목마를 예로 들면, 회전목마와 함께 회전하는 관찰자는 회전목마가 정지해 있다고 생각하지만, 지면에 서 있는 관찰자는 회전목마가 회전하는 것을 볼 수 있다.^[33]

회전목마에서 공을 던지는 상황을 생각해 보자. 회전목마와 함께 회전하는 관찰자(왼쪽 그림)는 공이 왼쪽으로 휘어져 날아가는 것처럼 보인다. 이는 공에 왼쪽 방향으로 작용하는 가상의 힘, 즉 코리올리 힘이 작용하기 때문이다. 반면, 지면에 서 있는 관찰자(오른쪽 그림)에게는 공이 직선으로 날아가는 것처럼 보인다. 이는 관성 좌표계에서는 물체에 작용하는 알짜힘이 0이면 물체가 등속 직선 운동을 하기 때문이다.

지구 표면 위를 "미끄러지는" 공기의 운동에 영향을 미치는 가속도는 코리올리 항의 수평 성분이며, 다음과 같이 주어진다.

:

-2 \, \boldsymbol{\omega \times  v}

이 성분은 지구 표면 위의 속도에 수직이며 다음 식으로 표현된다.

:

\omega \, v\  2 \, \sin \phi

여기서

$\omega$ 는 지구의 자전 속도이다.
$\phi$ 는 위도이며, 북반구에서는 양수이고 남반구에서는 음수이다.

북반구에서는 위에서 보았을 때 이 가속도가 운동 방향의 오른쪽으로 향하고, 남반구에서는 왼쪽으로 향한다.

코리올리 효과는 해양과 대기의 대규모 운동에 큰 영향을 미친다. 기상학과 해양학에서는 지구가 정지해 있는 회전 좌표계를 가정하는 것이 편리하며, 이 때 원심력과 코리올리 힘이 도입된다. 이 힘들의 상대적인 중요성은 로스비 수에 의해 결정된다. 예를 들어, 토네이도는 로스비 수가 높아 원심력은 크지만 코리올리 힘은 무시할 수 있다.^[35]

표층 해류는 바람의 영향으로 발생하며, 코리올리 힘은 해류와 사이클론의 이동에도 영향을 준다. 많은 해류는 환류라고 불리는 따뜻하고 고기압인 지역을 중심으로 순환하는데, 코리올리 효과에 의한 편향은 이러한 환류에서 나선형 패턴을 만든다. 또한, 나선형 바람 패턴은 허리케인 형성에 영향을 주며, 코리올리 효과가 강할수록 바람이 더 빠르게 회전하여 허리케인의 강도가 강해진다.^[36]

고기압 내의 공기는 코리올리 힘이 안쪽으로 향하는 방향으로 회전하여 바깥쪽으로 향하는 기압 경도력과 균형을 이룬다. 결과적으로 북반구의 고기압 주변에서는 시계 방향으로, 남반구에서는 반시계 방향으로 공기가 이동한다. 저기압 주변의 공기는 반대 방향으로 회전하여 코리올리 힘이 바깥쪽으로 향하고 안쪽으로 향하는 기압 경도력과 균형을 이룬다.^[37]

대기 중에 저기압 영역이 형성되면 공기는 그쪽으로 흘러들어가지만, 코리올리 힘에 의해 속도에 수직으로 휘어진다. 그러면 원형 운동 또는 사이클론성 흐름을 만드는 평형 시스템이 형성될 수 있다. 로스비 수가 낮기 때문에 힘의 균형은 저기압 영역을 향하는 기압경도력과 저기압 중심에서 멀어지는 코리올리 힘 사이에서 크게 결정된다.

기압 경도를 따라 흐르는 대신, 대기와 해양의 대규모 운동은 기압 경도에 수직으로 발생하는 경향이 있는데, 이를 지균풍이라고 한다.^[38] 자전하지 않는 행성에서는 유체가 가장 직선적인 경로를 따라 흐르며 기압 경도를 빠르게 제거하지만, 지균 평형은 관성 운동과 매우 다르며, 중위도 사이클론이 관성 원 운동보다 규모가 훨씬 큰 이유를 설명한다.

이러한 편향 패턴과 이동 방향을 뷔스발롯의 법칙이라고 한다. 대기에서는 흐름 패턴을 사이클론이라고 하며, 북반구에서는 저기압 영역 주변의 이동 방향이 시계 반대 방향이다. 남반구에서는 회전 역학이 거울상이기 때문에 이동 방향이 시계 방향이다.^[39] 고고도에서는 바깥쪽으로 퍼지는 공기가 반대 방향으로 회전한다.^[40] 적도에서는 코리올리 효과가 약하기 때문에 사이클론이 거의 발생하지 않는다.^[41]

4. 1. 1. 회전하는 벡터의 속도

회전하는 좌표계에서 벡터의 속도는 회전 각속도와 벡터의 외적으로 표현된다.^[33]

:

\boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ \cos \varphi \\ \sin \varphi \end{pmatrix}\ ,

\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ ,

:

\boldsymbol{ a}_C =-2\boldsymbol{\Omega \times v}= 2\,\omega\, \begin{pmatrix} v_n \sin \varphi-v_u \cos \varphi \\ -v_e \sin \varphi \\ v_e \cos\varphi\end{pmatrix}\ .

대기 또는 해양 역학을 고려할 때, 수직 속도는 작고, 코리올리 가속도의 수직 성분 (

v_e \cos\varphi

)은 중력 가속도(g, 지구 표면 근처에서 약 9.81m/s2)에 비해 작다. 이러한 경우, 수평(동쪽 및 북쪽) 성분만 중요하다. 위 식을 수평면으로 제한하면 (''v_u'' = 0으로 설정):

:

\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n\end{pmatrix}\ ,

\boldsymbol{ a}_c = \begin{pmatrix} v_n \\ -v_e\end{pmatrix}\ f\ ,

여기서

f = 2 \omega \sin \varphi \,

는 코리올리 파라미터라고 한다.

''v_n'' = 0으로 설정하면 (양의 φ 및 ω에 대해) 동쪽 방향의 이동은 남쪽 방향의 가속도를 초래함을 즉시 알 수 있다. 마찬가지로, ''v_e'' = 0으로 설정하면 북쪽 방향의 이동은 동쪽 방향의 가속도를 초래한다. 일반적으로, 수평적으로 관찰하면, 가속도를 유발하는 운동의 방향을 따라 보면, 가속도는 항상 수평 방향에 관계없이 오른쪽으로 90° 회전하고 크기가 같다.

적도 운동의 경우, φ = 0°로 설정하면:

:

\boldsymbol{ \Omega} = \omega \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}\ ,

\boldsymbol{ v} = \begin{pmatrix} v_e \\ v_n \\ v_u \end{pmatrix}\ ,

\boldsymbol{ a}_C = -2\boldsymbol{\Omega \times v} = 2\,\omega\, \begin{pmatrix} -v_u \\0 \\ v_e \end{pmatrix}\ .

이 경우 '''Ω'''는 북-남 축과 평행하다.

따라서 동쪽 방향의 운동(즉, 구의 회전 방향과 같은 방향)은 에트뵈시 효과라고 알려진 위쪽 방향의 가속도를 제공하고, 위쪽 방향의 운동은 서쪽 방향의 가속도를 생성한다.^[34]

4. 2. 회전하는 좌표계에서 벡터의 속도와 가속도

원점을 같이 쓰는 두 좌표계 x, y, z와 x', y', z'에서 벡터

\mathbf{r}

은 다음과 같이 표시된다.

\mathbf{r} = x\hat x  + y\hat y  + z\hat z

(x, y, z 좌표)

\mathbf{r} = x'\hat x'  + y'\hat y'  + z'\hat z'

(x', y', z' 좌표계)

벡터의 내적을 이용하면 x, y, z를 (

\ x', \hat x', \hat x

.), (

\ y', \hat y', \hat y

.), (

\ z', \hat z', \hat z

.)으로 표현할 수 있다.

회전좌표계에서는 원점을 기준으로 좌표축 x', y', z'이 회전한다. 서로 다른 좌표계에서 상대적인 속도는 다음과 같다.

\frac{d\mathbf{A}}{dt} =   \frac{d\mathbf{A'}}{dt} + V

::

=\mathbf{v'}+ V

::

=\mathbf{\dot{A_x'}} \hat \mathbf{x'} +\mathbf{\dot{A_y'}} \hat \mathbf{y'} +\mathbf{\dot{A_z'}} \hat \mathbf{z'} +\mathbf{A_x'}\frac{d\mathbf{\hat x'}}{dt} + \mathbf{A_y'}\frac{d\mathbf{\hat y'}}{dt}+\mathbf{A_z'}\frac{d\mathbf{\hat z'}}{dt}

이를 바탕으로 회전좌표계에서 x', y', z'의 단위벡터 회전을 적용하여 표현하면 다음과 같다.

\frac{d\mathbf{A}}{dt} =   \frac{d'\mathbf{A}}{dt} +\mathbf{A_x'}(\mathbf{\Omega} \times \mathbf{\hat x'}) + \mathbf{A_y'}(\mathbf{\Omega} \times \mathbf{\hat y'}) + \mathbf{A_z'}(\mathbf{\Omega} \times \mathbf{\hat z'})

::

= \frac{d'\mathbf{A}}{dt} +\mathbf{\Omega} \times (\mathbf{A_x'}\mathbf{\hat x'} + \mathbf{A_y'}\mathbf{\hat y'} + \mathbf{A_z'}\mathbf{\hat z'})

::

= \frac{d'\mathbf{A}}{dt} +\mathbf{\Omega} \times \mathbf{A}

따라서 축의 회전에 따른 속도는

\frac{d\mathbf{A}}{dt} = \frac{d'\mathbf{A}}{dt} +\mathbf{\Omega} \times \mathbf{A}

이다.

4. 2. 1. 회전하는 좌표계에서 벡터의 가속도

회전하는 좌표계에서 벡터의 가속도는 관성 좌표계에서의 가속도, 코리올리 힘, 원심력, 가로 힘의 합으로 표현된다. 회전 좌표계에서 벡터 A의 시간에 대한 2차 미분은 다음과 같이 나타낼 수 있다.

:

\frac{d^2\mathbf{A}}{dt^2} = \frac{d'^2\mathbf{A}}{dt^2} + 2\mathbf{\Omega} \times \frac{d'\mathbf{A}}{dt} + \mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{A}) + \frac{d\mathbf{\Omega}}{dt} \times \mathbf{A}

여기서

$\frac{d'^2\mathbf{A}}{dt^2}$ 는 회전 좌표계에서의 가속도
$2\mathbf{\Omega} \times \frac{d'\mathbf{A}}{dt}$ 는 코리올리 힘에 의한 가속도
$\mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{A})$ 는 원심력에 의한 가속도
$\frac{d\mathbf{\Omega}}{dt} \times \mathbf{A}$ 는 가로 힘에 의한 가속도

이다.

위 그림은 회전판 위에서 공을 던지는 상황을 나타낸다. 회전목마와 함께 회전하는 관찰자(왼쪽)는 공이 코리올리 힘과 원심력의 영향을 받아 휘어져 보이는 궤적을 그리며, 정지한 관찰자(오른쪽)는 공이 직선 경로를 따라 움직이는 것으로 관찰한다.

4. 3. 코리올리 정리 및 코리올리 힘

뉴턴의 운동 방정식을 회전하는 좌표계에 적용하면, 실제 힘뿐만 아니라 추가적인 항들이 나타난다. 이러한 항들은 회전 좌표계에서 나타나는 가상의 힘이며, 그중 하나가 코리올리 힘이다. 코리올리 힘은 회전하는 좌표계에서 물체의 운동을 기술할 때 운동 방정식에 추가되는 항으로 나타난다.^[16]

4. 3. 1. 코리올리 힘

뉴턴의 운동방정식이 x, y, z 좌표계에서 성립한다고 가정하면, 회전하는 x', y', z' 좌표계에서는 다음과 같은 식이 성립한다.^[16]

:

\mathbf{F} = m\frac{d'^2\mathbf{r}}{dt^2} + 2m\mathbf{\Omega} \times \frac{d'\mathbf{r}}{dt} + m\mathbf{\Omega} \times (\mathbf{\Omega} \times \mathbf{r}) + m\frac{d\mathbf{\Omega}}{dt} \times \mathbf{r}

이 식에서 우변의 두 번째 항이 코리올리 힘(Coriolis Force)이다. 세 번째 항은 원심력(Centripetal Force), 네 번째 항은 가로 힘(Transverse Force)이며 회전 각속도가 일정하지 않은 경우에만 나타난다.^[20] 원심력과 코리올리 힘을 도입하면 회전 좌표계에서의 운동방정식은 고정 좌표계와 같아진다. 원심력과 코리올리 힘은 실제 힘이 아니라 회전 좌표계에서 나타나는 가상의 힘(Fictitious Force)이다.

뉴턴 역학에서 관성 기준틀에 있는 물체의 운동 방정식은 다음과 같다.

:

\boldsymbol{F} = m\boldsymbol{a}

여기서

\boldsymbol{F}

는 물체에 작용하는 물리적 힘의 벡터 합,

m

은 물체의 질량,

\boldsymbol{a}

는 관성 기준틀에 대한 물체의 가속도이다.

이 방정식을 회전 기준틀로 변환하면 다음과 같은 형태가 된다.

:

\begin{align}\boldsymbol{F'} &=\boldsymbol{F} - m\frac{\mathrm{d} \boldsymbol{\omega}}{\mathrm{d}t}\times\boldsymbol{r'} - 2m \boldsymbol{\omega}\times \boldsymbol{v'} - m\boldsymbol{\omega} \times (\boldsymbol{\omega} \times \boldsymbol{r'})  \\& = m\boldsymbol{a'}\end{align}

여기서 '프라임'(') 변수는 회전 기준틀의 좌표를 나타내며(미분이 아님), 각 변수는 다음과 같다.

$\boldsymbol{F}$ : 물체에 작용하는 물리적 힘의 벡터 합
$\boldsymbol{\omega}$ : 관성 기준틀에 대한 회전 기준틀의 각속도
$\boldsymbol{r'}$ : 회전 기준틀에 대한 물체의 위치 벡터
$\boldsymbol{v'}$ : 회전 기준틀에 대한 물체의 속도
$\boldsymbol{a'}$ : 회전 기준틀에 대한 물체의 가속도

회전 틀에서 인지되는 겉보기 힘은 실제 외부 힘과 마찬가지로 겉보기 가속도에 기여하는 추가적인 힘으로 작용한다.^[17]^[18]^[19] 방정식의 겉보기 힘 항은 왼쪽에서 오른쪽으로 읽으면 오일러 힘, 코리올리 힘, 원심력 순서이다.

코리올리 힘은 회전 각속도와 물체의 속도의 외적에 비례하며, 물체의 질량에 비례한다. 비회전 관성 기준틀

(\boldsymbol\omega=0)

의 경우 코리올리 힘과 다른 모든 겉보기 힘은 사라진다.^[21]

코리올리 힘은 두 벡터의 외적에 비례하므로, 물체의 속도와 좌표계의 회전 벡터 모두에 수직이다. 따라서 다음과 같은 특징을 갖는다.

속도가 회전축과 평행하면 코리올리 힘은 0이다.
속도가 축을 향해 직선으로 안쪽으로 향하면 코리올리 힘은 국지적 회전 방향과 같다.
속도가 축에서 직선으로 바깥쪽으로 향하면 코리올리 힘은 국지적 회전 방향과 반대이다.
속도가 회전 방향이면 코리올리 힘은 축에서 바깥쪽으로 향한다.
속도가 회전 방향과 반대이면 코리올리 힘은 축 안쪽으로 향한다.

5. 코리올리 힘의 예

코리올리 힘은 지구의 자전으로 인해 발생하는 현상으로, 대기와 해양의 순환에 큰 영향을 미친다.

코리올리 효과는 주로 수평 운동으로 발생하는 수평 가속도 성분에 의해 나타난다. 서쪽으로 이동하는 물체는 아래쪽으로, 동쪽으로 이동하는 물체는 위쪽으로 편향되는데, 이를 에트뵈시 효과라고 한다.^[43] 에트뵈시 효과는 적도 부근에서 가장 크다. 대기에서는 바람이 정수압 평형에서 약간 벗어나는데, 열대 대기에서는 이 압력 편차가 작아 에트뵈시 효과가 압력 편차에 미치는 영향이 크다.^[44]

위나 아래로 움직이는 물체는 각각 서쪽이나 동쪽으로 편향된다. 이 효과는 적도 부근에서 가장 크며, 수직 운동은 보통 범위와 지속 시간이 제한적이어서 효과가 작고 정밀한 기기로 측정해야 한다. 하지만 우주선 궤도 진입처럼 운동량이 크게 변할 때는 이 효과가 중요해진다. 가장 빠르고 연료 효율이 좋은 궤도 진입 경로는 적도에서 발사해 동쪽으로 향하는 곡선 경로이다.

적도에서 마찰 없이 움직이는 기차를 예로 들어 코리올리 효과를 설명할 수 있다. 기차가 서쪽으로 가면 지구 회전 방향과 반대로 움직여 코리올리 힘이 아래쪽으로 작용, 무게가 더 무겁게 느껴진다. 정지하면 코리올리 힘은 0이 되어 평소 무게를 회복한다. 동쪽으로 가면 코리올리 힘이 위쪽으로 작용해 더 가볍게 느껴진다.^[47]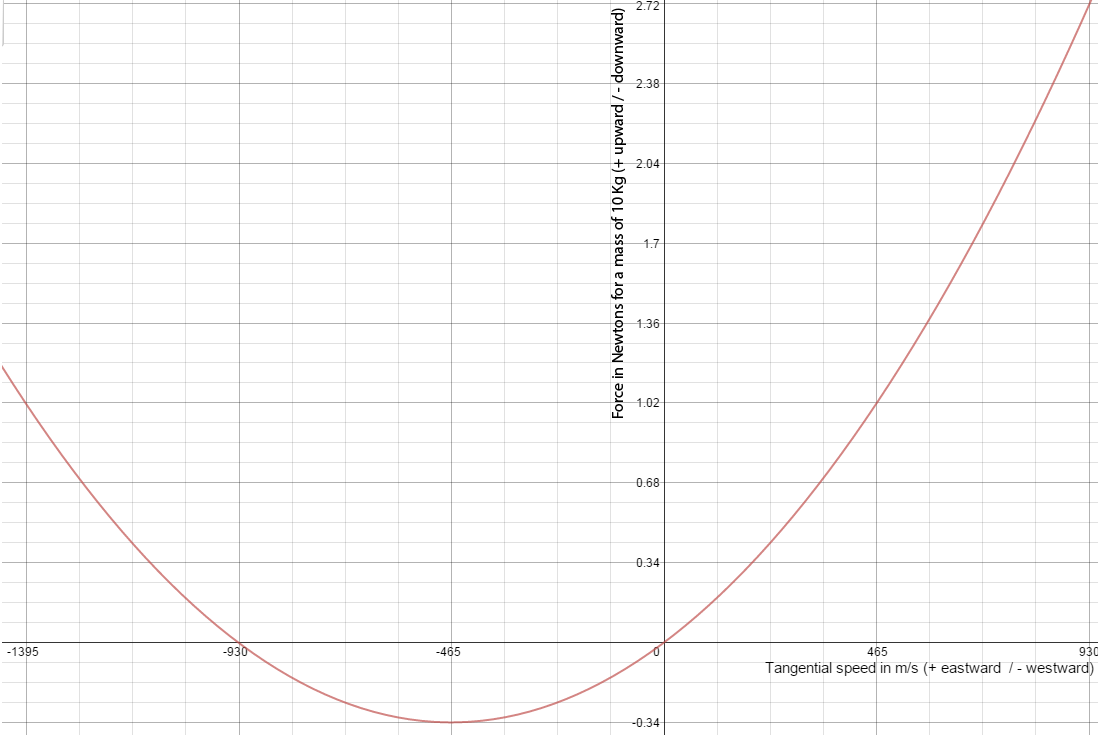

지구 적도를 따라 움직이는 물체가 느끼는 힘 (회전 좌표계 기준). 양의 힘은 위쪽, 양의 속도는 동쪽, 음의 속도는 서쪽.

이는 서쪽으로 가는 고속 발사체가 아래로, 동쪽으로 가는 발사체가 위로 휘는 이유를 설명하며, 이를 에트뵈시 효과라 한다.^[48]

코리올리 효과는 외부탄도학에서 장거리 포탄 탄도 계산에 중요하며, 제1차 세계 대전 당시 독일군이 파리를 폭격한 파리포가 대표적 예시다. 코리올리 효과는 탄환 탄도를 미세하게 바꿔 정확도에 영향을 주므로, 장거리 사수는 이를 보정해야 한다. 예를 들어 새크라멘토에서 북쪽으로 발사된 탄환은 오른쪽으로 휜다.^[58]^[59]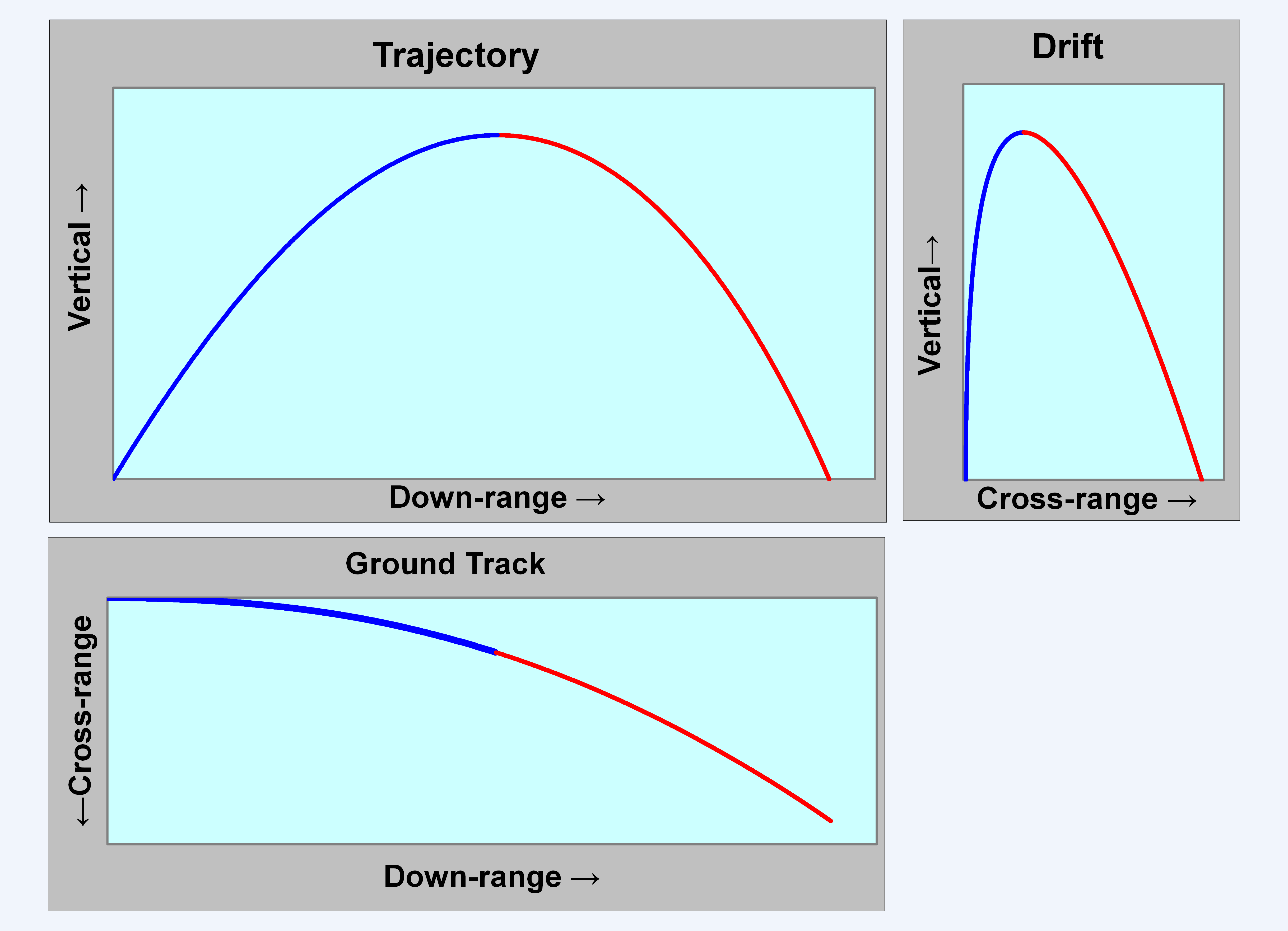

움직이는 발사체에 작용하는 코리올리 힘은 다음과 같이 계산된다.^[61]

:

A_\mathrm{X} = -2 \omega ( V_\mathrm{Y} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z}  \sin \theta_\mathrm{lat} )

:

A_\mathrm{Y} = 2 \omega ( V_\mathrm{X} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z}  \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})

:

A_\mathrm{Z} = 2 \omega ( V_\mathrm{X} \sin \theta_\mathrm{lat}  - V_\mathrm{Y}  \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})

각 변수는 다음과 같다.

변수	설명
$A_\mathrm{X}$	사거리 가속도
$A_\mathrm{Y}$	수직 가속도 (양수는 위쪽)
$A_\mathrm{Z}$	횡거리 가속도 (양수는 오른쪽)
$V_\mathrm{X}$	사거리 속도
$V_\mathrm{Y}$	수직 속도 (양수는 위쪽)
$V_\mathrm{Z}$	횡거리 속도 (양수는 오른쪽)
$\omega$	지구 각속도 ( 항성일 기준)
$\theta_\mathrm{lat}$	위도 (양수는 북반구)
$\phi_\mathrm{az}$	방위각 (북쪽에서 시계 방향)

5. 0. 1. 북반구에서의 바람의 우측 편향

북반구에서 바람은 코리올리 힘에 의해 진행 방향의 오른쪽으로 편향된다. 이는 각운동량 보존 법칙으로 설명할 수 있다. 적도에서 북풍이 부는 경우를 예로 들어보자. 지구는 둥글기 때문에 바람이 북쪽(고위도)으로 이동할수록 자전축과의 거리가 가까워진다. 각운동량은 보존되어야 하므로, 거리가 줄어들면 각속도가 증가해야 한다. 따라서 바람은 상대적으로 각속도가 빨라져 동쪽으로 편향, 즉 진행 방향의 오른쪽으로 휘게 된다.^[42]

이러한 현상으로 인해 북반구에서 저기압은 반시계 방향으로 회전하고, 고기압은 시계 방향으로 회전한다.

5. 0. 2. 푸코의 진자

푸코의 진자. $\mathbf{w}$ 각속도(푸코 진자의 수평 방향 각속도)로 회전하는 계에서 보았을 때 진자는 단순히 단진자 운동을 하는 것을 알 수 있다.

푸코의 진자는 코리올리 힘의 영향을 받아 진동면이 회전하는 현상을 보여주는 대표적인 예시이다. 푸코의 진자는 어떤 수직면에서 자유롭게 흔들리는 줄에 매달린 추로 구성된다. 진자는 처음에 정확한 수직면에서 흔들리기 시작하지만, 시간이 지남에 따라 진동면이 천천히 회전한다.

코리올리 힘은 회전하는 좌표계에서 운동하는 물체에 작용하는 가상의 힘이다. 지구는 자전하기 때문에 지구 표면에서 움직이는 물체는 코리올리 힘의 영향을 받는다. 푸코의 진자의 경우, 코리올리 힘은 진자를 수평 방향으로 움직이게 하여 진동면이 회전하게 만든다.

푸코 진자의 진동면 회전 속도는 지구의 자전 각속도와 위도에 따라 달라진다. 북반구에서 푸코의 진자는 시계 방향으로 회전하며, 그 각속도(

\mathbf{w}

)는

w = -\mathbf{\Omega} \cos \theta

로 주어진다. 여기서

\mathbf{\Omega}

는 지구의 자전 각속도이고,

\theta

는 지구 축과 수직 사이의 각(위도)이다.

흔히 욕조나 변기에서 물이 빠질 때 북반구와 남반구에서 서로 다른 방향으로 회전한다는 오해가 있지만, 이는 사실이 아니다. 이러한 작은 규모에서는 코리올리 효과가 매우 미미하여 물의 회전 방향에 영향을 주지 못한다.^[49]^[50]^[51]^[52] 실제로는 배수구와 용기의 형태, 물의 초기 운동 상태 등 다른 요인들이 물의 회전 방향을 결정한다.^[53]^[54]^[55]

하지만 1962년 매사추세츠 공과대학교(MIT)의 애셔 섀피로(Ascher H. Shapiro)는 매우 정밀하게 통제된 실험 조건에서 코리올리 효과를 관찰하는 데 성공했다.^[56] 그는 지름 2미터의 큰 물통에 물을 채우고 최소 24시간 동안 안정시킨 후, 배수구 위에 작은 나무 십자형 표시를 설치하여 물이 빠지는 동안의 회전을 관찰했다. 그 결과, 북반구에서 물은 시계 반대 방향으로 회전하는 것을 확인했다.

로이드 트레페선(Lloyd Trefethen)은 시드니 대학교에서 유사한 실험을 수행하여 남반구에서 시계 방향의 회전을 보고했다.^[57]

6. 지구에의 응용

코리올리 힘은 지구 표면에서 움직이는 물체, 특히 대기와 해양의 대규모 운동에 큰 영향을 미친다.

코리올리 효과의 실질적인 영향은 주로 수평 운동에 의해 생성되는 수평 가속도 성분에 의해 발생하지만, 다른 요소들도 존재한다. 예를 들어 서쪽으로 이동하는 물체는 아래쪽으로, 동쪽으로 이동하는 물체는 위쪽으로 편향되는데, 이를 에트뵈시 효과라고 한다.^[43] 에트뵈시 효과는 적도 부근에서 가장 크다. 에트뵈시 효과에 의해 생성되는 힘은 수평 성분과 유사하지만, 중력과 압력으로 인한 훨씬 더 큰 수직력으로 인해 정수압 평형에서는 중요하지 않다. 그러나 열대 대기에서는 압력 편차의 크기가 매우 작아 에트뵈시 효과의 압력 편차에 대한 기여가 상당하다.^[44]

또한, 위쪽이나 아래쪽으로 이동하는 물체는 각각 서쪽 또는 동쪽으로 편향된다. 이 효과 역시 적도 근처에서 가장 크다. 수직 운동은 일반적으로 제한된 범위와 지속 시간을 가지므로, 효과의 크기는 작고 이를 감지하려면 정밀한 기기가 필요하다. 예를 들어, 이상적인 수치 모델링 연구에 따르면, 이 효과는 대기 중 장기간(2주 이상) 가열 또는 냉각이 주어지면 열대 대규모 풍장에 약 10% 정도 직접적으로 영향을 미칠 수 있다.^[45]^[46]

적도에서 마찰이 없는 철로 위를 달리는 기차를 예로 들어보자. 기차가 하루(465 m/s) 만에 지구를 한 바퀴 도는 데 필요한 속도로 움직인다고 가정할 때,^[47] 코리올리 효과는 다음과 같이 세 가지 경우로 나누어 살펴볼 수 있다.

# 기차가 서쪽으로 이동하는 경우: 기차는 지구 회전 방향과 반대로 움직이므로 코리올리 힘은 지구 중심 방향(아래쪽)으로 작용한다. 따라서 기차는 정지해 있을 때보다 더 무겁게 느껴진다.

# 기차가 정지하는 경우: 지구 회전 좌표계에서 기차의 속도는 0이므로 코리올리 힘도 0이 되어 기차와 승객은 평소 무게를 회복한다.

# 기차가 동쪽으로 이동하는 경우: 기차는 지구 회전 방향으로 움직이므로 코리올리 힘은 지구 중심 반대 방향(위쪽)으로 작용한다. 따라서 기차는 정지해 있을 때보다 더 가볍게 느껴진다.

이는 서쪽으로 발사된 발사체가 아래로, 동쪽으로 발사된 발사체가 위로 편향되는 이유를 설명하며, 코리올리 효과의 이 수직 성분을 에트뵈시 효과라고 한다.^[48]

코리올리 효과는 외부탄도학에서 매우 장거리 포병 포탄의 탄도를 계산하는 데 중요하다. 가장 유명한 역사적 예로는 제1차 세계대전 당시 독일군이 약 120km 거리에서 파리를 폭격하는 데 사용한 파리포가 있다. 코리올리 효과는 미세하게 탄환의 탄도를 변경하여 매우 먼 거리에서 정확도에 영향을 미친다. 정확한 장거리 사격을 하는 저격수들은 이를 보정한다. 캘리포니아주 새크라멘토의 위도에서 1000yd 북쪽으로 발사된 탄환은 오른쪽으로 2.8in 휘어진다. 위에서 설명한 에트뵈시 효과 때문에 서쪽으로 발사된 탄환은 낮게, 동쪽으로 발사된 탄환은 높게 명중한다.^[58]^[59]

움직이는 발사체에 작용하는 코리올리 힘은 세 방향 모두의 속도 성분, 위도 및 방위각에 따라 달라진다. 방향은 일반적으로 사거리(총이 처음 가리키는 방향), 수직 및 횡거리이다.^[61]

: $A_\mathrm{X} = -2 \omega ( V_\mathrm{Y} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z} \sin \theta_\mathrm{lat} )$

: $A_\mathrm{Y} = 2 \omega ( V_\mathrm{X} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z} \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})$

: $A_\mathrm{Z} = 2 \omega ( V_\mathrm{X} \sin \theta_\mathrm{lat} - V_\mathrm{Y} \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})$

여기서 각 항목은 다음과 같다.

$A_\mathrm{X}$ : 사거리 가속도.
$A_\mathrm{Y}$ : 수직 가속도(양수는 위쪽 가속도를 나타냄).
$A_\mathrm{Z}$ : 횡거리 가속도(양수는 오른쪽 가속도를 나타냄).
$V_\mathrm{X}$ : 사거리 속도.
$V_\mathrm{Y}$ : 수직 속도(양수는 위쪽을 나타냄).
$V_\mathrm{Z}$ : 횡거리 속도(양수는 오른쪽 속도를 나타냄).
$\omega$ = 0.00007292 rad/sec: 지구의 각속도(항성일 기준).
$\theta_\mathrm{lat}$ : 위도(양수는 북반구를 나타냄).
$\phi_\mathrm{az}$ : 북쪽에서 시계 방향으로 측정한 방위각.

6. 1. 회전하는 구

지구는 회전하는 구체이므로, 코리올리 힘은 위도에 따라 다르게 나타난다. 지구 자전에 의한 코리올리 힘의 크기는 물체의 속도를

v

라고 할 때 다음과 같이 표현된다.^[87]^[88]

:

|\boldsymbol{F}_{\mathrm{C}}|=mvf,\quad f=2\omega \sin \phi

여기서

f

는 코리올리 인자라고 불리며,

\omega

는 지구의 자전 속도,

\phi

는 위도를 나타낸다. 북반구에서는

\phi

가 양수이고, 남반구에서는 음수이다.

북반구에서는 코리올리 힘이 운동 방향의 오른쪽으로, 남반구에서는 왼쪽으로 작용한다. 이는 지구가 동쪽으로 자전하기 때문인데, 저위도에서 고위도로 이동하는 물체는 동쪽으로, 고위도에서 저위도로 이동하는 물체는 서쪽으로 힘을 받는다.

코리올리 효과는 일상생활에서는 매우 작게 나타나지만, 대규모 운동(운동 속도가 크고, 운동 시간이 긴)에서는 큰 영향을 미친다. 예를 들어, 북극점에서 초속 1000m로 10km 거리까지 포탄을 쏘았을 때, 코리올리 힘에 의해 약 7.3m 정도의 궤도 변화가 발생한다.^[118]^[119]

코리올리 효과는 탄도학에서 장거리 포탄의 탄도를 계산하는 데 매우 중요하다. 예를 들어, 제1차 세계 대전 중 독일군이 약 120km 거리에서 파리를 포격하기 위해 사용한 파리포의 경우, 코리올리 효과는 포탄의 궤적을 미세하게 변화시켜 명중률에 영향을 미쳤다.

이동하는 포탄에 작용하는 코리올리 힘은 위도, 방위각의 3방향 모든 속도 성분에 의존하며, 일반적으로 다운레인지(처음 총이 향한 방향), 수직 방향, 크로스레인지의 3방향으로 나타난다.^[121]

:

A_\mathrm{X} = -2 \omega ( V_\mathrm{Y} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z}  \sin \theta_\mathrm{lat} )

:

A_\mathrm{Y} = 2 \omega ( V_\mathrm{X} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z}  \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})

:

A_\mathrm{Z} = 2 \omega ( V_\mathrm{X} \sin \theta_\mathrm{lat}  - V_\mathrm{Y}  \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})

각 항목은 다음과 같다.

$A_\mathrm{X}$ : 다운레인지 가속도
$A_\mathrm{Y}$ : 수직 방향의 가속도, 양수는 위쪽 가속도를 나타낸다.
$A_\mathrm{Z}$ : 크로스레인지 가속도, 양수는 오른쪽 가속도를 나타낸다.
$V_\mathrm{X}$ : 다운레인지의 속도
$V_\mathrm{Y}$ : 연직 방향의 속도, 양수는 위쪽 속도를 나타낸다.
$V_\mathrm{Z}$ : 크로스레인지의 속도, 양수는 오른쪽 속도를 나타낸다.
$\omega$ = 0.00007292 rad/sec: 지구의 각속도 (항성일 기준)
$\theta_\mathrm{lat}$ : 위도, 양수는 북반구를 나타낸다.
$\phi_\mathrm{az}$ : 진북에서 시계 방향으로 측정한 방위각.

6. 2. 기상학과 해양학

코리올리 효과는 대기 순환과 해류와 같은 대규모 흐름에 큰 영향을 미쳐, 제트 기류나 서쪽 경계류와 같은 뚜렷한 특징을 형성한다. 이러한 현상들은 코리올리 힘과 압력 경도력이 서로 균형을 이루는 지균평형 상태에 놓여있다.^[86]

지衡풍: 상공에서 기압차가 발생하면, 공기는 기압이 높은 곳에서 낮은 곳으로 이동하려는 기압경도력을 받는다. 등압선이 평행하고 기압경도력이 일정하면, 공기는 등압선에 직각 방향으로 가속된다. 이때 북반구에서는 코리올리 힘이 진행 방향의 오른쪽으로 작용하여 공기는 오른쪽으로 휘면서 속도가 증가한다. 최종적으로 기압경도력과 코리올리 힘이 균형을 이루면, 공기는 일정한 방향과 속도를 유지하는 안정된 바람, 즉 지衡풍이 된다.
해류: 해류의 움직임 역시 코리올리 힘의 영향을 받는다. (에크만 수송)

이 외에도 코리올리 힘은 로스비 파나 켈빈 파와 같이 해양과 대기에서 나타나는 다양한 파동의 전파에도 영향을 미치며, 해양의 에크만 층이나 스베르드룹 균형과 같은 대규모 해류 패턴을 형성하는 데에도 중요한 역할을 한다.

6. 2. 1. 저기압 영역 주변의 흐름

저기압 영역에서는 바람이 중심으로 불어 들어오면서 코리올리 힘의 영향을 받는다. 코리올리 힘은 운동 방향에 대해 북반구에서는 오른쪽, 남반구에서는 왼쪽으로 작용하기 때문에, 바람의 방향이 편향된다.^[86]

북반구: 바람이 저기압 중심으로 향하면서 오른쪽으로 휘어져, 결과적으로 반시계 방향의 회전 흐름이 만들어진다.
남반구: 바람이 저기압 중심으로 향하면서 왼쪽으로 휘어져, 결과적으로 시계 방향의 회전 흐름이 만들어진다.

이러한 회전 흐름은 태풍과 같은 소용돌이 현상에서 뚜렷하게 나타난다. 태풍이 북반구에서 반시계 방향으로 회전하는 것은 이러한 코리올리힘의 작용 때문이다.

6. 2. 2. 관성 원

코리올리 힘만 작용하는 속도

v\,

로 움직이는 공기 또는 물 덩어리는 '관성원'이라고 하는 원형 궤적을 따라 이동한다. 힘이 입자의 운동 방향에 대해 직각으로 작용하기 때문에, 입자는 반지름

R

인 원을 일정한 속도로 이동하는데, 이 반지름은 다음과 같이 주어진다.

:

R = \frac{v}{f}

여기서

f

는 코리올리 매개변수

2 \Omega \sin \varphi

이며(

\varphi

는 위도), 질량이 완전한 원을 완성하는 데 걸리는 시간은 따라서

2\pi/f

이다. 코리올리 매개변수는 중위도에서 일반적으로 약 10⁻⁴ s⁻¹의 값을 가지므로, 전형적인 대기 속도 10m/s의 경우 반지름은 100km이고 주기는 약 17시간이다. 전형적인 속도가 10cm/s인 해류의 경우, 관성원의 반지름은 1km이다. 이러한 관성원은 북반구에서는 시계 방향(궤적이 오른쪽으로 휘어짐)이고 남반구에서는 시계 반대 방향이다.^[42]

회전계가 포물선 회전판인 경우,

f

는 일정하고 궤적은 정확한 원이 된다. 회전하는 행성에서는

f

가 위도에 따라 변하고 입자의 경로는 정확한 원을 형성하지 않는다. 매개변수

f

가 위도의 사인 함수로 변하기 때문에, 주어진 속도와 관련된 진동의 반지름은 극지방(위도 ±90°)에서 가장 작고 적도 방향으로 증가한다.^[42]

6. 2. 3. 기타 지구 효과

코리올리 효과는 대규모 해양 순환과 대기 순환에 큰 영향을 미쳐 제트 기류와 서쪽 경계류와 같은 뚜렷한 특징을 형성한다. 이러한 특징들은 지균평형 상태에 있는데, 이는 코리올리 힘과 압력 경도력이 서로 균형을 이룬다는 것을 의미한다.^[86] 코리올리 가속도는 로스비 파와 켈빈 파를 포함한 해양과 대기에서 여러 유형의 파동 전파에도 영향을 미친다. 또한 해양의 에크만 층 역학과 스베르드룹 균형이라고 하는 대규모 해류 패턴 형성에도 중요한 역할을 한다.

지衡풍: 상공에서 기압차가 있으면 기압이 높은 쪽에서 낮은 쪽으로 공기를 움직이려는 기압경도력이 작용한다. 등압선이 평행하고 기압경도력이 일정하면 공기는 등압선에 대해 직각으로 가속된다. 북반구에서는 진행 방향 오른쪽으로 코리올리 힘이 작용하여 공기는 오른쪽으로 휘면서 속도가 빨라지고, 최종적으로 기압경도력과 코리올리 힘이 균형을 이루어 방향과 속도가 일정한 안정된 바람이 된다.
태풍: 태풍이 북반구에서 시계 반대 방향으로 소용돌이치는 것은, 바람이 저기압 중심으로 향할 때 코리올리의 힘을 받아 진행 방향에 대해 중심에서 오른쪽으로 치우친 지점에 도달하기 때문이다.^[86]
극궤도 인공위성: 북극점 상공에서 일본 상공으로 향하려는 인공위성은 직진하지만, 지구는 자전하기 때문에 지상 관측자에게는 위성이 아시아 대륙 쪽으로 벗어나는 것처럼 보인다.
해류: 해류의 운동도 코리올리의 힘의 영향을 받는다(에크만 수송).
포탄: 북반구에서 정북으로 쏜 포탄이 표적보다 약간 동쪽(오른쪽)으로 벗어나는 것은 옛날부터 알려진 사실이다. 대포, 로켓, 1000m에 가까운 장거리 저격 등의 궤도 계산에는 코리올리의 힘을 고려한 보정이 필요하다.

지구의 각속도를

\omega

라고 하면, 위도

\phi

에서 지평면 내 남북 방향 벡터의 각속도는

\omega \sin \phi

가 된다.^[87]^[88] 따라서 지구 자전에 의한 코리올리 힘의 크기는 물체의 속도를

v

라고 하면

:

|\boldsymbol{F}_{\mathrm{C}}|=mvf,\quad f=2\omega \sin \phi

로 표현된다.

f

는 코리올리 인자라고 불린다.

코리올리 힘의 영향을 보여주는 예로, 북극점에서 시속 100km의 공을 18.4m 거리에서 던졌을 때, 코리올리 힘에 의한 가속도는

:

a' = 2\omega v' =4.03\times 10^{-3} ~ \mathrm{m/s^2}

이다. 걸리는 시간

t

는

t=0.661 ~ \mathrm{s}

이므로, 어긋나는 거리

x

는

:

x= {1 \over 2}a't^2\fallingdotseq 0.88 ~ \mathrm{mm}

로 1mm에도 미치지 않는다. 북극점보다 위도가 낮은 지역에서는 코리올리의 힘의 영향은 더 작아진다.

반면, 북극점에서 초속 1000m의 포탄을 10km까지 쏘았을 때, 코리올리 힘에 의한 가속도는

:

a' = 2\omega v' =1.46\times 10^{-1} ~ \mathrm{m/s^2}

이고, 걸리는 시간 ''t''는

t=10.0 ~ \mathrm{s}

이므로, 어긋나는 거리

x

는

:

x= {1 \over 2}a't^2\fallingdotseq 7.3 ~ \mathrm{m}

로 7m의 어긋남이 생긴다. 이처럼 대규모 운동에서는 코리올리의 힘이 큰 영향을 미친다.

코리올리 효과의 또 다른 요소로 에트뵈시 효과(Eötvös effect)가 있는데, 서쪽으로 이동하는 물체는 아래로, 동쪽으로 이동하는 물체는 위로 편향되는 현상이다.^[103] 이 효과는 적도 부근에서 최대가 된다. 열대 대기에서는 에트뵈시 효과가 압력 편차에 상당한 영향을 준다.^[104]

상승 또는 하강하는 물체도 각각 서쪽 또는 동쪽으로 편향되며, 이 영향 역시 적도 부근에서 최대이다. 수직 이동은 범위와 시간이 제한적이므로 영향은 작지만, 장기간의 대기 가열/냉각이 있는 경우 열대 풍속장에 영향을 줄 수 있다.^[105]^[106] 궤도 발사 우주선처럼 운동량 변화가 큰 경우, 적도에서 정동으로 발사하는 것이 가장 효율적이다.

적도에서 마찰 없는 레일 위를 달리는 열차를 예로 들어, 코리올리 효과를 세 가지 경우로 나누어 설명할 수 있다.

\left(1\text{ day} \mathrel\overset{\land}{=} 8\text{ s}\right):

# 열차가 서쪽으로 진행하는 경우: 지구 자전과 반대 방향이므로 코리올리 힘은 지구 중심 방향(아래쪽)이다. 열차는 정지 상태보다 0.34%^[107] 더 큰 힘을 받는다.

# 열차가 정지해 있는 경우: 코리올리 힘은 0이다.

# 열차가 동쪽으로 진행하는 경우: 코리올리 힘은 지구 중심 반대 방향(위쪽)이다. 열차는 더 가볍게 느껴진다.

이는 서쪽으로 날아가는 총알이 아래로, 동쪽으로 날아가는 총알이 위로 편향되는 이유를 설명하며, 이 수직 성분을 에트뵈시 효과라고 한다.^[108]

물체의 속도가 지구 자전 속도(465m/s)보다 빨라지면 서쪽으로 갈수록 에트뵈시 효과가 감소한다. 서쪽으로 향하는 열차가 속도를 높이면, 구심력 때문에 레일을 누르는 힘이 감소한다. 열차 속도가 자전 속도의 두 배가 되면 에트뵈시 효과가 상쇄된다. 그 이상의 속도에서는 위쪽 힘이 작용한다. 에트뵈시 효과는 대칭적이지 않아, 고속으로 서쪽으로 이동하는 물체가 받는 아래쪽 힘이 같은 속도로 동쪽으로 이동하는 물체가 받는 위쪽 힘보다 작다.

6. 3. 에트뵈시 효과

Eötvös effect^영어는 동서 방향으로 이동하는 물체가 수직 방향으로 힘을 받는 현상이다. 동쪽으로 이동하는 물체는 위쪽으로, 서쪽으로 이동하는 물체는 아래쪽으로 힘을 받는다.^[43]

이는 코리올리 효과의 한 요소로, 적도 부근에서 가장 크게 나타난다. 서쪽으로 이동하는 물체는 아래쪽으로, 동쪽으로 이동하는 물체는 위쪽으로 편향된다.^[48]

에트뵈시 효과는 지구의 회전에 의해 발생한다. 지구는 동쪽으로 자전하고 있기 때문에, 동쪽으로 이동하는 물체는 지구의 자전 속도에 더해져 더 큰 원심력을 받게 되고, 결과적으로 위쪽으로 힘을 받는다. 반대로 서쪽으로 이동하는 물체는 지구의 자전 속도에서 상쇄되어 원심력이 감소하고, 아래쪽으로 힘을 받는다.

예를 들어, 적도에서 마찰이 없는 철로 위를 달리는 기차를 생각해 보자.^[47]

기차가 서쪽으로 이동하는 경우: 기차는 지구 자전 방향과 반대로 움직이므로 코리올리 힘은 아래쪽으로 작용한다. 이로 인해 기차는 더 무거워진다.
기차가 정지해 있는 경우: 코리올리 힘은 작용하지 않아 기차는 원래 무게를 유지한다.
기차가 동쪽으로 이동하는 경우: 기차는 지구 자전 방향으로 움직이므로 코리올리 힘은 위쪽으로 작용한다. 이로 인해 기차는 더 가벼워진다.

이러한 현상은 고속으로 발사되는 발사체에서도 나타난다. 서쪽으로 발사된 발사체는 아래로, 동쪽으로 발사된 발사체는 위로 편향된다.^[58]^[59]

에트뵈시 효과는 대규모의 운동에서 두드러지게 나타난다. 예를 들어, 장거리 포탄의 궤적을 계산하거나, 인공위성을 궤도에 진입시킬 때 이 효과를 고려해야 한다.

7. 다른 분야에서의 코리올리 효과

코리올리 효과는 외부탄도학에서 매우 장거리 포병 포탄의 탄도를 계산하는 데 중요하게 사용된다. 가장 유명한 역사적 사례는 제1차 세계 대전 당시 독일군이 약 120km 거리에서 파리를 포격하는 데 사용한 파리포이다.^[58]^[59] 코리올리 효과는 포탄의 탄도를 미세하게 변경하여 매우 먼 거리에서 정확도에 영향을 미친다. 따라서 저격수와 같이 정확한 장거리 사수는 이를 보정해야 한다. 예를 들어 캘리포니아주 새크라멘토의 위도에서 약 914.40m 북쪽으로 발사된 탄환은 오른쪽으로 약 7.11cm 휘어진다. 또한, 서쪽으로 발사된 탄환은 낮게, 동쪽으로 발사된 탄환은 높게 명중하는 수직 성분도 존재한다.^[58]^[59]

움직이는 발사체에 작용하는 코리올리 힘은 세 방향 모두의 속도 성분, 위도 및 방위각에 따라 달라진다. 일반적인 방향은 사거리, 수직 및 횡거리이다.^[61]

: $A_\mathrm{X} = -2 \omega ( V_\mathrm{Y} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z} \sin \theta_\mathrm{lat} )$

: $A_\mathrm{Y} = 2 \omega ( V_\mathrm{X} \cos \theta_\mathrm{lat} \sin \phi_\mathrm{az} + V_\mathrm{Z} \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})$

: $A_\mathrm{Z} = 2 \omega ( V_\mathrm{X} \sin \theta_\mathrm{lat} - V_\mathrm{Y} \cos \theta_\mathrm{lat} \cos \phi_\mathrm{az})$

각 항목은 다음과 같다.

변수	설명
$A_\mathrm{X}$	사거리 가속도
$A_\mathrm{Y}$	수직 가속도 (양수는 위쪽 가속도)
$A_\mathrm{Z}$	횡거리 가속도 (양수는 오른쪽 가속도)
$V_\mathrm{X}$	사거리 속도
$V_\mathrm{Y}$	수직 속도 (양수는 위쪽)
$V_\mathrm{Z}$	횡거리 속도 (양수는 오른쪽)
$\omega$	지구의 각속도 (항성일 기준, 0.00007292rad/sec)
$\theta_\mathrm{lat}$	위도 (양수는 북반구)
$\phi_\mathrm{az}$	북쪽에서 시계 방향으로 측정한 방위각

피겨 스케이터처럼 회전하면서 추를 든 손을 앞으로 뻗었다가 가슴에 가져다 대는 동작을 반복하면 코리올리 효과를 실감할 수 있다. 왼쪽으로 회전하는 경우, 팔을 앞으로 뻗을 때 추가 오른쪽으로 당겨지는 듯한 느낌이 들고, 팔을 가슴에 가져다 댈 때는 왼쪽으로 당겨지는 듯한 느낌을 받는다. 이처럼 추의 진행 방향에서 오른쪽으로 치우치는 힘이 코리올리 힘이다.

이러한 코리올리 효과는 각속도를 측정하는 자이로스코프나 유량계 등에 공학적으로 이용된다.

7. 1. 코리올리 유량계

코리올리 유량계는 코리올리 효과를 응용하여 유체의 질량유량과 밀도를 측정하는 질량유량계의 일종이다.^[65]^[122] 작동 원리는 유체가 통과하는 관에 진동을 유도하는 것이다. 이 진동은 완전한 원형은 아니지만, 코리올리 효과를 발생시키는 회전하는 기준틀을 제공한다. 유량계의 설계에 따라 구체적인 방법은 다르지만, 센서는 진동하는 유량 튜브의 주파수, 위상 변화 및 진폭의 변화를 모니터링하고 분석한다. 관찰된 변화는 유체의 질량 유량과 밀도를 나타낸다.^[65]^[122]

7. 2. 분자 물리학

다원자 분자에서 분자 운동은 강체 회전과 평형 위치를 중심으로 한 원자들의 내부 진동으로 설명할 수 있다. 원자의 진동으로 인해 원자들은 분자의 회전 좌표계에 대해 상대적으로 운동한다. 따라서 코리올리 효과가 나타나 원자들이 원래의 진동에 수직인 방향으로 움직이게 된다. 이는 회전과 진동 준위 사이의 분자 스펙트럼 혼합으로 이어지며, 이를 통해 코리올리 결합 상수를 결정할 수 있다.^[66]^[123]

7. 3. 자이로스코프 세차 운동

회전하는 자이로스코프에 스핀 축에 직각인 축을 따라 외부 힘이 가해지면, 스핀과 관련된 림(rim) 속도는 외부 힘의 축에 대해 방사 방향으로 향하게 된다. 이로 인해 자이로스코프의 림에 외부 힘에 의한 힘이 작용하여 외부 힘이 자이로스코프를 기울이는 방향과 직각으로 자이로스코프가 기울어지게 된다. 이러한 경향은 회전하는 물체를 그 회전 프레임에 유지하는 효과를 갖는다.

7. 4. 곤충 비행

파리(쌍시목)와 일부 나방(인시목)은 비행 중 코리올리 효과를 이용하여 몸의 각속도에 대한 정보를 얻는다. 이들은 특수한 부속지나 기관을 통해 코리올리 힘을 감지한다. 파리의 경우, 날개 바로 뒤에 위치한 아령 모양의 기관인 "할터레"가 이 역할을 한다.^[67]

파리의 할터레는 주 날개와 같은 박동 주파수로 평면에서 진동한다. 몸체가 회전하면 할터레가 운동 평면에서 측면으로 편향되는 방식으로 코리올리 힘을 감지한다.^[68]

나방의 경우, 더듬이가 파리의 할터레와 유사하게 코리올리 힘을 감지하는 역할을 한다.^[69] 파리와 나방 모두 부속지 기저부의 기계수용기 집합은 피치 및 롤 평면의 회전에 상관하는 박동 주파수에서의 편향과, 요 평면의 회전에 상관하는 두 배의 박동 주파수에서의 편향에 민감하다.^[70]^[69]

7. 5. 라그랑주점 안정성

천문학에서 라그랑주점은 중력만을 받는 작은 천체가 두 개의 큰 천체에 대해 상대적으로 안정된 위치를 유지할 수 있는 다섯 개의 위치이다. 처음 세 개의 라그랑주점(L₁, L₂, L₃)은 두 큰 천체를 잇는 선상에 위치하며, 나머지 두 점(L₄와 L₅)은 각각 두 큰 천체와 정삼각형을 이룬다. L₄와 L₅점은 두 큰 천체와 함께 회전하는 좌표계에서 유효퍼텐셜의 최댓값에 해당하지만, 코리올리 효과 때문에 안정적이다.^[71] 이러한 안정성으로 인해 L₄ 또는 L₅ 주위를 도는 궤도, 즉 말굽형 궤도가 생길 수 있으며, 트로이군 소행성이 발견될 수 있다. 또한 L₃, L₄, L₅를 둘러싸는 궤도, 즉 말발굽 궤도가 생길 수도 있다.

참조

_[1] 서적 The Mechanical Universe: Mechanics and Heat, Advanced Edition https://books.google[...] Cambridge University Press
_[2] 학술지 Coriolis effect, two centuries before Coriolis
_[3] 학술지 The Coriolis Effect Further Described in the Seventeenth Century 2016-11-24
_[4] 서적 Essays in the History of Mechanics Springer Science & Business Media
_[5] 학술지 The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885
_[6] 서적 Tides: A Scientific History https://books.google[...] Cambridge University Press
_[7] 학술지 Sur les équations du mouvement relatif des systèmes de corps https://babel.hathit[...]
_[8] 학술지 How Do We Understand the Coriolis Force? 1998-07-01
_[9] 서적 A History of Mechanics https://books.google[...] Courier Dover Publications
_[10] 서적 A Treatise on Infinitesimal Calculus : Vol. IV. The dynamics of material systems https://books.google[...] Oxford : University Press
_[11] 서적 The Dynamics of Particles and of Rigid, Elastic, and Fluid Bodies https://archive.org/[...] B. G. Teubner
_[12] 학술지 Space, Time, and Gravitation https://books.google[...]
_[13] 학술지 An Essay on the Winds and the Currents of the Ocean https://web.archive.[...] 2009-01-01
_[14] 학술지 The Coriolis Effect:Four centuries of conflict between common sense and mathematics, Part I: A history to 1885 https://journal.mete[...] Swedish Meteorological and Hydrological Institute 2024-05-27
_[15] 학술지 A brief history of the Coriolis force 2012
_[16] 서적 Classical Mechanics: With introduction to Nonlinear Oscillations and Chaos Narosa Publishing House
_[17] 서적 A Universe of Atoms, an Atom in the Universe https://books.google[...] Springer
_[18] 문서
_[19] 서적 Essential Classical Mechanics https://books.google[...] World Scientific Publishing Company 2021-03-13
_[20] 서적 The Variational Principles of Mechanics https://books.google[...] Dover Publications
_[21] 서적 Contemporary Physics and the Limits of Knowledge https://books.google[...] Rutgers University Press
_[22] 서적 Setting Aside All Authority: Giovanni Battista Riccioli and the Science Against Copernicus in the Age of Galileo https://books.google[...] University of Notre Dame Press
_[23] 서적 Solar Energy at Urban Scale https://books.google[...] John Wiley & Sons
_[24] 서적 Energy and the Environment: Resources, Technologies, and Impacts https://books.google[...] Verve Publishers
_[25] 웹사이트 MIT: Flow in rotating environments https://ocw.mit.edu/[...]
_[26] 학술지 Debunking Coriolis Force Myths
_[27] 웹사이트 Coriolis Force Effect on Drains https://www.snopes.c[...] 2003-04-28
_[28] 서적 Numerical Models of Oceans and Oceanic Processes https://books.google[...] Academic Press
_[29] 서적 Variational Principles in Classical Mechanics University of Rochester River Campus Libraries 2021-08-19
_[30] 서적 Science of Earth Systems https://books.google[...] Thomson Delmar Learning
_[31] 서적 An Introduction to Dynamic Meteorology https://books.google[...] Academic Press
_[32] 서적 Ballistics: Theory and Design of Guns and Ammunition https://books.google[...] CRC Press
_[33] 서적 Geophysical Theory https://books.google[...] Columbia University Press
_[34] 학술지 The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885
_[35] 서적 An Introduction to Dynamic Meteorology https://books.google[...] Elsevier Academic Press
_[36] 웹사이트 What Is the Coriolis Effect? https://www.thoughtc[...]
_[37] 뉴스 The Coriolis Effect: Earth's Rotation and Its Effect on Weather National Geographic Society 2023-05-02
_[38] 서적 Atmosphere, Weather and Climate https://books.google[...] Routledge-Taylor & Francis
_[39] 웹사이트 Tropical Cyclones (Hurricanes) http://www.tulane.ed[...] Tulane University 2014-09-01 # Fall 2014를 9월 1일로 가정
_[40] 웹사이트 Cloud Spirals and Outflow in Tropical Storm Katrina from Earth Observatory https://photojournal[...] NASA
_[41] 서적 Encyclopedia of Disaster Relief https://books.google[...] SAGE Publications 2010-12-29
_[42] 서적 Atmosphere, Ocean and Climate Dynamics: An Introductory Text https://books.google[...] Elsevier Academic Press
_[43] 서적 Fundamentals of Geophysics https://books.google[...] Cambridge University Press
_[44] 학술지 Nontraditional hypsometric equation 2020
_[45] 학술지 The Importance of the Nontraditional Coriolis Terms in Large-Scale Motions in the Tropics Forced by Prescribed Cumulus Heating 2012
_[46] 학술지 Linear effects of nontraditional Coriolis terms on intertropical convergence zone forced large-scale flow 2019
_[47] 학술지 The Coriolis Effect – a conflict between common sense and mathematics http://met.no/englis[...] The Swedish Meteorological and Hydrological Institute
_[48] 서적 A Student's Guide to Geophysical Equations https://books.google[...] Cambridge University Press 2011
_[49] 웹사이트 Can Somebody Finally Settle This Question: Does Water Flowing Down a Drain Spin in Different Directions Depending on Which Hemisphere You're In? And If So, Why? https://www.scientif[...] Scientific American-Springer Nature 2001-01-28
_[50] 웹사이트 Bad Coriolis... Bad Meteorology http://www.ems.psu.e[...]
_[51] 웹사이트 Flush Bosh http://www.snopes.co[...] 2003-04-28
_[52] 웹사이트 Does the rotation of the Earth affect toilets and baseball games? http://science.howst[...] 2009-07-20
_[53] 서적 Physics: A World View https://books.google[...] Cengage Learning
_[54] 학술지 Stationary bathtub vortices and a critical regime of liquid discharge http://eprints.usq.e[...]
_[55] 서적 A Student's Guide to Earth Science: Words and terms https://books.google[...] Greenwood Publishing Group
_[56] 학술지 Bath-Tub Vortex 1962-12-01 # December 1962를 12월 1일로 가정
_[57] 학술지 The Bath-Tub Vortex in the Southern Hemisphere 1965-09-01 # September 1965를 9월 1일로 가정
_[58] 서적 Classical Mechanics https://books.google[...] University Science Books
_[59] 뉴스 Do Snipers Compensate for the Earth's Rotation? https://www.washingt[...] 2010-06-25
_[60] 서적 Ocean Circulation in Three Dimensions Cambridge University Press 2019
_[61] 간행물 Modern Exterior Ballistics Schiffer Military History
_[62] 웹사이트 Geophysical fluid dynamics lab demonstration https://web.archive.[...] 2005-11-20
_[63] 웹사이트 Brian Fiedler https://web.archive.[...] 2006-03-21
_[64] 서적 Atmosphere, Ocean, and Climate Dynamics: An Introductory Text https://books.google[...] Academic Press
_[65] 웹사이트 Mass Flowmeters http://www.omega.com[...]
_[66] 서적 Vibrational states Wiley
_[67] 학술지 Halteres of Flies as Gyroscopic Organs of Equilibrium 1938-05-21
_[68] 학술지 Haltere-mediated equilibrium reflexes of the fruit fly, Drosophila melanogaster
_[69] 학술지 Antennal mechanosensors mediate flight control in moths http://www.hep.princ[...] 2007-02-01 # February 2007를 2월 1일로 가정
_[70] 학술지 A neural basis for gyroscopic force measurement in the halteres of Holorusia
_[71] 서적 Encyclopedia of the Solar System https://books.google[...] Elsevier
_[72] 학술지 Coriolis effect, two centuries before Coriolis
_[73] 학술지 The Coriolis Effect Further Described in the Seventeenth Century 2016-11-24
_[74] 서적 Essays in the History of Mechanics Springer Science & Business Media
_[75] 학술지 The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885
_[76] 서적 Tides: A Scientific History https://books.google[...] Cambridge University Press
_[77] 학술지 Sur les équations du mouvement relatif des systèmes de corps https://babel.hathit[...]
_[78] 학술지 How Do We Understand the Coriolis Force? https://journals.ame[...] 1998-07-01
_[79] 서적 A History of Mechanics https://books.google[...] Courier Dover Publications
_[80] 서적 A Treatise on Infinitesimal Calculus : Vol. IV. The dynamics of material systems https://books.google[...] Oxford : University Press
_[81] 서적 The Dynamics of Particles and of Rigid, Elastic, and Fluid Bodies https://archive.org/[...] B. G. Teubner
_[82] 학술지 Space, Time, and Gravitation https://books.google[...]
_[83] 학술지 An Essay on the Winds and the Currents of the Ocean https://web.archive.[...] 2009-01-01
_[84] 학술지 The Coriolis Effect:Four centuries of conflict between common sense and mathematics, Part I: A history to 1885 Swedish Meteorological and Hydrological Institute 2006-02-26
_[85] 학술지 A brief history of the Coriolis force 2012
_[86] 서적 物理学読本みすず書房 1981
_[87] 문서 緯度φの地平面内の南北方向の単位方向ベクトルの１日の回転運動
_[88] 문서 「角速度」を「回転軸方向のベクトル」と捉え、コリオリの力を「ベクトル積」で考える場合
_[89] 서적 Solar Energy at Urban Scale https://books.google[...] John Wiley & Sons
_[90] 서적 Energy and the Environment: Resources, Technologies, and Impacts https://books.google[...] Verve Publishers
_[91] 웹사이트 MIT: Flow in rotating environments https://web.archive.[...] 2023-07-06
_[92] 학술지 Debunking Coriolis Force Myths
_[93] 웹사이트 Coriolis Force Effect on Drains https://www.snopes.c[...]
_[94] 서적 Geophysical Theory https://books.google[...] Columbia University Press
_[95] 서적 An Introduction to Dynamic Meteorology https://books.google[...] Elsevier Academic Press
_[96] 웹사이트 What Is the Coriolis Effect? https://www.thoughtc[...] 2023-07-06
_[97] 뉴스 The Coriolis Effect: Earth's Rotation and Its Effect on Weather https://www.national[...] National Geographic Society 2018-01-17
_[98] 서적 Atmosphere, Weather and Climate https://books.google[...] Routledge-Taylor & Francis
_[99] 웹사이트 Tropical Cyclones (Hurricanes) http://www.tulane.ed[...] Tulane University 2016-12-24
_[100] 웹사이트 Cloud Spirals and Outflow in Tropical Storm Katrina from Earth Observatory https://photojournal[...] NASA 2023-07-06
_[101] 서적 Encyclopedia of Disaster Relief https://books.google[...] SAGE Publications 2010-12-29
_[102] 서적 Atmosphere, Ocean and Climate Dynamics: An Introductory Text https://books.google[...] Elsevier Academic Press
_[103] 서적 Fundamentals of Geophysics https://books.google[...] Cambridge University Press
_[104] 학술지 Nontraditional hypsometric equation 2020
_[105] 학술지 The Importance of the Nontraditional Coriolis Terms in Large-Scale Motions in the Tropics Forced by Prescribed Cumulus Heating 2012
_[106] 논문 Linear effects of nontraditional Coriolis terms on intertropical convergence zone forced large‐scale flow 2019
_[107] 논문 The Coriolis Effect – a conflict between common sense and mathematics http://met.no/englis[...] The Swedish Meteorological and Hydrological Institute 2005-09-06
_[108] 서적 A Student's Guide to Geophysical Equations https://books.google[...] Cambridge University Press 2020-02-25
_[109] 웹사이트 Can Somebody Finally Settle This Question: Does Water Flowing Down a Drain Spin in Different Directions Depending on Which Hemisphere You're In? And If So, Why? https://www.scientif[...] Scientific American-Springer Nature 2023-06-28
_[110] 웹사이트 Bad Coriolis... Bad Meteorology http://www.ems.psu.e[...] 2023-06-28
_[111] 웹사이트 Flush Bosh http://www.snopes.co[...] 2016-12-21
_[112] 웹사이트 Does the rotation of the Earth affect toilets and baseball games? http://science.howst[...] 2016-12-21
_[113] 서적 Physics: A World View https://books.google[...] Cengage Learning
_[114] 논문 Stationary bathtub vortices and a critical regime of liquid discharge http://eprints.usq.e[...]
_[115] 서적 A Student's Guide to Earth Science: Words and terms https://books.google[...] Greenwood Publishing Group
_[116] 논문 Bath-Tub Vortex 1962-12
_[117] 논문 The Bath-Tub Vortex in the Southern Hemisphere 1965-09
_[118] 서적 Classical Mechanics https://books.google[...] University Science Books
_[119] 뉴스 Do Snipers Compensate for the Earth's Rotation? https://www.washingt[...] 2010-06-25
_[120] 서적 Ocean Circulation in Three Dimensions Cambridge University Press 2019-08-19
_[121] 서적 Modern Exterior Ballistics Schiffer Military History
_[122] 웹사이트 Mass Flowmeters http://www.omega.com[...]
_[123] 서적 Vibrational states Wiley
_[124] 논문 Halteres of Flies as Gyroscopic Organs of Equilibrium 1938-05-21
_[125] 논문 Haltere-mediated equilibrium reflexes of the fruit fly, Drosophila melanogaster
_[126] 논문 Antennal mechanosensors mediate flight control in moths http://www.hep.princ[...] 2017-12-01
_[127] 논문 A neural basis for gyroscopic force measurement in the halteres of Holorusia
_[128] 서적 Encyclopedia of the Solar System https://books.google[...] Elsevier

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com